Espero y tengan una Feliz Navidad y un próspero año nuevo
2015...
Física 5to año Sección “U”
Aprende Física de una manera práctica, didáctica y divertida…
martes, 9 de diciembre de 2014
jueves, 4 de diciembre de 2014
aplicaciones de la ley de coulomb
Ley de Coulomb
El
físico francés Charles Coulomb investigó en la década de 1780 la
relación cuantitativa de las fuerzas eléctricas entre objetos cargados.
Su ley la demostró usando una balanza de torsión, que él mismo inventó,
identificando cómo varía la fuerza eléctrica en función de la magnitud
de las cargas y de la distancia entre ellas.
La ley de Coulomb establece:
• -Que
la magnitud de cada una de las fuerzas eléctricas con que interactúan
dos cargas puntuales en reposo es proporcional al producto de la
magnitud de ambas cargas e inversamente proporcional al cuadrado de la
distancia que las separa.
• -Es
decir: Si tenemos dos cargas (carga 1 y carga 2) que están separadas
una distancia r, la fuerza que ejercen entre ellas es igual a la carga 1
multiplicada por la carga 2, dividida entre la distancia al cuadrado.
La Ley de Coulomb se expresa mejor con magnitudes vectoriales:
El exponente (de la distancia: d) de la Ley de Coulomb es, hasta donde se sabe hoy en día, exactamente 2. Experimentalmente se sabe que, si el exponente fuera de la forma : 1. entonces: 2. =
Ley de coulomb y sus aplicaciones .

Una
manifestación habitual de la electricidad es la fuerza de atracción o
repulsión entre dos cuerpos estacionarios que, de acuerdo con el
principio de acción y reacción, ejercen la misma fuerza eléctrica uno
sobre otro. La carga eléctrica de cada cuerpo puede medirse en
culombios. La fuerza entre dos partículas con cargas q1 y q2 puede
calcularse a partir de la ley de Coulomb
Según la cual la fuerza es proporcional al producto de las cargas dividido entre el cuadrado de la distancia que las separa. La constante de proporcionalidad K depende del medio que rodea a las cargas.
Según la cual la fuerza es proporcional al producto de las cargas dividido entre el cuadrado de la distancia que las separa. La constante de proporcionalidad K depende del medio que rodea a las cargas.
Esta
ley permite encontrar el valor numérico de la fuerza de atracción o
repulsión entre dos o más cuerpos, para ello se utiliza la siguiente
ecuación:
ECUACION: sirve para hallar le fuerza entre dos o más cuerpos.
Fe= q1 q2
R2
Fe: fuerza eléctrica.
K: constante dieléctrica.
q1 y q2: carga eléctrica.
R: distancia que separa las cargas.
"Las fuerzas
que se ejercen entre dos cargas eléctricas son directamente
proporcional a sus cantidades de electricidad e inversamente
proporcionales al cuadrado de la distancia que las separa".
F= (k)qq1/r2
k = 9 x 109 Nm2/C2
q q1 = cargas del electrón (C)
r2 = distancia al cuadrado (m2)
F = fuerza (N)
F= (k)qq1/r2
k = 9 x 109 Nm2/C2
q q1 = cargas del electrón (C)
r2 = distancia al cuadrado (m2)
F = fuerza (N)
Donde K es la constante de Coulomb, q1 y q2 son los valores de las cargas y r2 es la distancia que separa las cargas.
Utilizando
una balanza de torsión elaborada por el mismo, enuncio la ley que lleva
su nombre “La ley de Coulomb”, la cual establece:
1º Las cargas eléctricas de un signo contrario se atraen y las de signos iguales se repelen.
2º La fuerza de atracción o de repulsión es directamente proporcional ala carga de cada cuerpo e inversamente proporcional a la de cuadrado que los separa.
1º Las cargas eléctricas de un signo contrario se atraen y las de signos iguales se repelen.
2º La fuerza de atracción o de repulsión es directamente proporcional ala carga de cada cuerpo e inversamente proporcional a la de cuadrado que los separa.
APLICACIÓN DE LA LEY DE COULOMB
Ley de Coulomb
El
físico francés Charles Coulomb investigó en la década de 1780 la
relación cuantitativa de las fuerzas eléctricas entre objetos cargados.
Su ley la demostró usando una balanza de torsión, que él mismo inventó,
identificando cómo varía la fuerza eléctrica en función de la magnitud
de las cargas y de la distancia entre ellas.
La ley de Coulomb establece:
• -Que
la magnitud de cada una de las fuerzas eléctricas con que interactúan
dos cargas puntuales en reposo es proporcional al producto de la
magnitud de ambas cargas e inversamente proporcional al cuadrado de la
distancia que las separa.
• -Es
decir: Si tenemos dos cargas (carga 1 y carga 2) que están separadas
una distancia r, la fuerza que ejercen entre ellas es igual a la carga 1
multiplicada por la carga 2, dividida entre la distancia al cuadrado.
La Ley de Coulomb se expresa mejor con magnitudes vectoriales:
El exponente (de la distancia: d) de la Ley de Coulomb es, hasta donde se sabe hoy en día, exactamente 2. Experimentalmente se sabe que, si el exponente fuera de la forma : 1. entonces: 2. =
conductividad electrica y su relacion con el cuerpo humano
El cuerpo humano funciona con electricidad, funciona con electrones, de modo que, ingerimos comida por su potencial eléctrico, o porsu potencial de electrones.
Los alimentos que tomamos poseen energía química, que al consumirla se transforma en energía metabólica; por lo tanto, lo que comemos o bebemos afecta el medio internoy eso va a energizar o a debilitar nuestro cuerpo.
La electricidad en sí es invisible, sabemos que ésta allí, que se puede medir; y que la electricidad, también fluye por nuestro cuerpo. El hombrenecesita estar cargado en sentido físico como una pila. Si nuestra batería no está cargada, entonces daríamos a este estado el nombre de alguna enfermedad. Y la enfermedad no es más que un déficit deenergía, un déficit de actividad que se expresa en forma de un síntoma.
analisis vectorial
Sumario
En esta lección introduciremos el concepto de integral a lo largo de una curva de un
campo escalar, llamada también integral de línea respecto de la longitud de arco. El contenido
completo de esta lección se articula de la siguiente manera:
V.1.1 Curvas.
V.1.2 Longitud de una curva.
V.1.3 Integral de línea respecto de un campo escalar.
V.1.4 Propiedades de la integral de línea.
V.1.5 Interpretaciones de la integral de línea.
V.1.6 Relación de ejercicios.
Curvas en Rn
5.1.1.
Recordemos que una curva en Rn es una función continua γ : [a, b] −→ Rn . se
dice que dicha curva se dice regular si la curva γ es de clase C 1 en [a, b].
El ejemplo más sencillo de curva regular es el segmento:
Dados dos puntos x e y de Rn , se define el segmento de extremos x e y, [x, y],
como la curva
γ : [0, 1] −→ Rn ,
definida por γ(t) = (1 − t)x + ty.
En esta lección introduciremos el concepto de integral a lo largo de una curva de un
campo escalar, llamada también integral de línea respecto de la longitud de arco. El contenido
completo de esta lección se articula de la siguiente manera:
V.1.1 Curvas.
V.1.2 Longitud de una curva.
V.1.3 Integral de línea respecto de un campo escalar.
V.1.4 Propiedades de la integral de línea.
V.1.5 Interpretaciones de la integral de línea.
V.1.6 Relación de ejercicios.
Curvas en Rn
5.1.1.
Recordemos que una curva en Rn es una función continua γ : [a, b] −→ Rn . se
dice que dicha curva se dice regular si la curva γ es de clase C 1 en [a, b].
El ejemplo más sencillo de curva regular es el segmento:
Dados dos puntos x e y de Rn , se define el segmento de extremos x e y, [x, y],
como la curva
γ : [0, 1] −→ Rn ,
definida por γ(t) = (1 − t)x + ty.
relaciones trigonometrica.
Una relacion trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas
y es válida para todos los valores del ángulo en los que están
definidas las funciones (y las operaciones aritméticas involucradas).
Notación: se define sin2α como (sin α)2. Lo mismo se aplica a las demás funciones trigonométricas.
De estas dos identidades, se puede extrapolar la siguiente tabla. Sin
embargo, nótese que estas ecuaciones de conversión pueden devolver el
signo incorrecto (+ ó −). Por ejemplo, si  la conversión propuesta en la tabla indica que
la conversión propuesta en la tabla indica que 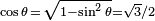 , aunque es posible que
, aunque es posible que  . Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ.
. Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ.
Notación: se define sin2α como (sin α)2. Lo mismo se aplica a las demás funciones trigonométricas.
| Relación pitagórica | 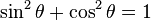 |
|---|---|
| Identidad de la razón |  |
 la conversión propuesta en la tabla indica que
la conversión propuesta en la tabla indica que 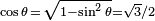 , aunque es posible que
, aunque es posible que  . Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ.
. Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ.| En términos de |  |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|
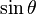 |
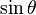 |
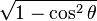 |
 |
 |
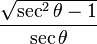 |
 |
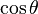 |
 |
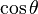 |
 |
 |
 |
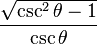 |
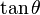 |
 |
 |
 |
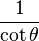 |
 |
 |
 |
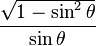 |
 |
 |
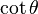 |
 |
 |
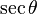 |
 |
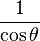 |
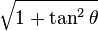 |
 |
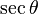 |
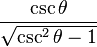 |
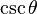 |
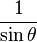 |
 |
 |
 |
 |
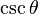 |
Suscribirse a:
Entradas (Atom)






